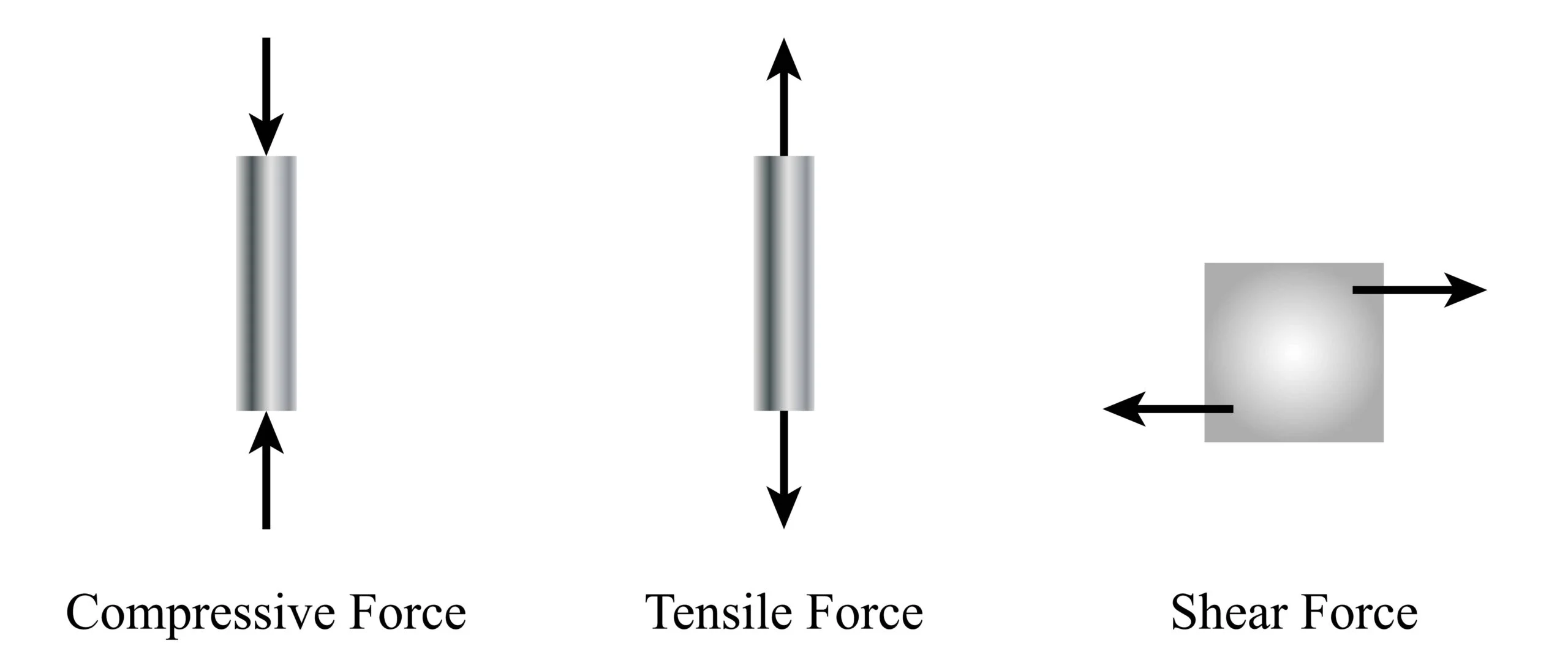
In the world of metalworking, fabricators, engineers, manufacturers, and machinists have to navigate the delicate balance between tensile and compressive forces. Though seemingly simple, these forces dictate the strength, durability, and resilience of most modern metal structures.
The strength of a metal plays a critical role in designing products or structural architectures. Key elements of metal strength include tensile strength, yield strength, hardness, and density. Understanding these properties is essential for predicting how a metal will perform under different conditions.
Tensile strength and yield strength are crucial for assessing a metal’s performance. Tensile strength measures the maximum amount of tensile stress a metal can withstand while being stretched or pulled before breaking.
Yield strength, on the other hand, is the tensile stress at which a material begins to deform plastically. Beyond this point, the material will not return to its original shape. The elastic limit, closely related to yield strength, defines the maximum extent to which a material can be deformed without permanent changes.
Dive deeper into the intricacies of tensile stress vs compressive stress and discover how to leverage these principles for your next project. Stay with us as we explore advanced concepts and practical insights that every fabricator, engineer, manufacturer, and machinist should have handy.
Tensile Strength vs Compressive Strength: A Quick Guide
Understanding the forces at play in metalworking is key to mastering the craft. Below, we’ll analyze the fascinating world of tensile and compressive stress, which shape the foundation of metal structures.
First, we’ll explore how tensile stresses stretch metals to their limits, revealing their strength and flexibility. Then, we’ll shift focus to compressive stress, uncovering how metals withstand intense pressure and maintain their integrity under load.
The Impact of Tensile Stresses on Metal Durability
When a metal stretches, it experiences tensile strength. Mathematically, tensile stress equals force/area. The maximum tensile stress a metal can handle represents its tensile strength. The stress-strain curve helps visualize this process, and a tensile test is often conducted to determine these tensile force properties.
Tensile strength is divided into yield strength and ultimate tensile strength. The first occurs when the metal is subjected to external tensile strength loading, causing it to undergo both plastic and elastic deformation.
The yield strength denotes the tensile strength force up to which a metal can regain its original shape once the force is removed.
The material’s yield strength is a key factor in this process. In many engineering applications, the proof stress is used to define the yield point, especially for materials that do not have a clear yield point. This helps determine the maximum stress a material can endure before permanent deformation occurs.
Beyond the yield point, the metal will continue to undergo plastic deformation until a point before necking takes place. This limit is known as the ultimate tensile strength.
In short, it represents the maximum tensile stress a metal can handle without breaking into two pieces. The stress strain curve clearly illustrates this stress value, highlighting the material’s yield and tensile strength characteristics.
Compressive Stress in Metals
Compressive stresses represent the maximum compression or pressure a metal can handle without breaking. This means that the length has been reduced compared to its original measure. Although tensile stresses and tensile strength measurements focus on a material’s stretching and breaking points under tension, they provide valuable insights that complement the understanding of compressive force and compressive load.
There are six different types of compressive failure modes:
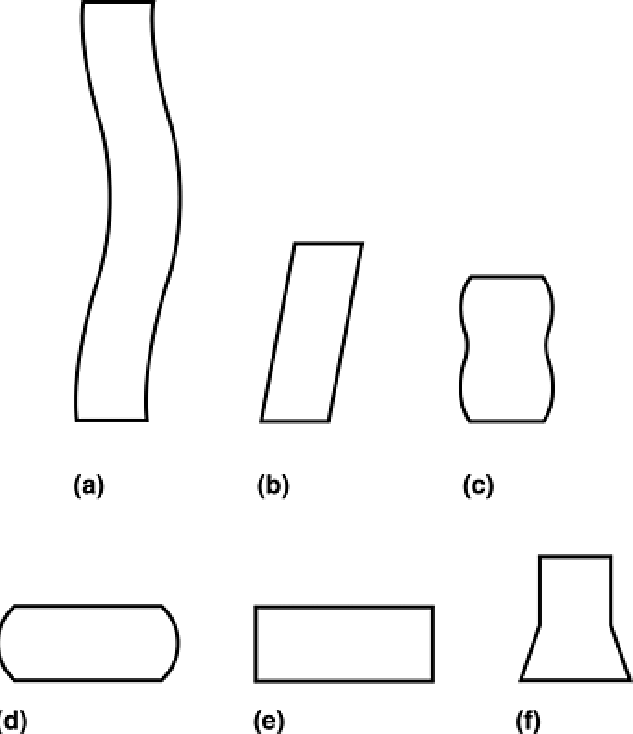
- Buckling: Sudden sideway change in original shape under an axial load
- Shearing: Sliding failure along the direction of applied stress
- Double barrelling: The formation of two barrels during the compression of high prismatic bodies without external zones
- Barrelling: The generation of a convex surface on the exterior of a cylinder
- Homogeneous compression: No friction is present at the contact surface
- Compressive instability: Failure due to work softening of the metal
A widely accepted test to determine the compressive strength under maximum applied stress is the Mohs hardness test. By understanding both tensile and compressive stresses, as well as their respective strengths and failure modes, metalworkers can better predict and enhance the performance of metal components under various loads.
The Role of Tensile Stress and Compressive Strength in Metal Selection
The maximum value of compressive strength and tensile strength varies between metals. Some metals show exceptional tensile strength under tension, whereas others are good at handling maximum compressive load.
Thus, comparing two metals under tension and compressive forces requires first acknowledging the intended application; only then can the metals be effectively compared.
This comparison often involves understanding the yield strength vs tensile strength of each metal and how the material’s resistance affects its performance.
The following table compares the tensile strength, yield strength, hardness, and density of various metals:
| Types of Metals | Tensile Strength (PSI) | Yield Strength (PSI) | Hardness Rockwell (B-Scale) | Density (Kg/m3) |
| Stainless Steel 304 | 90,000 | 40,000 | 88 | 8000 |
| Aluminum 6061-T6 | 45000 | 40000 | 60 | 2720 |
| Aluminum 5052-H32 | 33000 | 28000 | 2680 | |
| Aluminum 3003 | 22000 | 21000 | 20 to 25 | 2730 |
| Steel A36 | 58-80000 | 36000 | 7800 | |
| Steel Grade 50 | 65000 | 50000 | 7800 | |
| Yellow Brass | 40000 | 55 | 8470 | |
| Red Brass | 49000 | 65 | 8746 | |
| Copper | 28000 | 10 | 8940 | |
| Phosphor Bronze | 55000 | 78 | 8900 | |
| Aluminum Bronze | 27000 | 77 | 7700-8700 | |
| Titanium | 63000 | 37000 | 80 | 4500 |
Steel has higher tensile strength and yield strength than aluminum; however, aluminum is lightweight and offers better resistance to corrosion than steel. Thus, studying the parameters is important when considering the application requirements.
Also, a metal can have high tensile strength yet low compressive strength and vice versa. For instance, the compressive strength of cast iron is more than its tensile strength, but it’s the opposite of mild steel. Brittle materials like cast iron contain many voids.
Under tensile forces, these voids act as notches, resulting in a high propagation of cracks through the material. But these voids get closed under a compressive force, nullifying any possible crack propagation.
On the other hand, in ductile materials, cracks formed under the compressive stress load are closed easily without propagating through the material. As a result, these are equally strong in tension and compression; however, they tend to fail under shear stress.
Understanding the compressive strength limit of a material is crucial in applications where compressive loads are predominant. The ultimate compressive strength is a key parameter that indicates the maximum compressive stress a material can withstand.
By considering tensile stresses and compressive stresses together, engineers can design structures and components that utilize the strengths of different metals effectively.
The Importance of Understanding Yield Strength and Tensile Strength
Compression and tensile strength are very important properties of metals in engineering design. The main objective is to keep the plastic deformation and permanent deformation as small as possible.
A tensile test is crucial to accurately determining these strengths. In this regard, Young’s modulus measures the degree of plastic deformation of a material under lengthwise tension or compression.
Young’s modulus is another way of calculating the degree of deformation of a material under lengthwise tension or compression. It’s defined as the ratio between longitudinal tensile stress and strain. The higher the Young’s modulus, the stiffer the material, and the smaller the elastic deformation for a given applied load.
For example, constructing a house from a metal with a low Young’s modulus will deflect a lot under a compressive load; a stiffer metal would give a more desired response.
Modern vaulting poles are a great example of this. To maximize an athlete’s performance, a vaulting pole should be made of light materials and store elastic strain as the pole bends. Thus, these poles are constructed from fiberglass (E =15 GPa) or a mix of fiberglass and carbon fiber (E =500 GPa).
The Young’s modulus for some of the most commonly used metals is shown below:
| Material | Young’s Modulus (E) | |
| 106 psi | 109N/m2, GPa | |
| Aluminum | 10.0 | 69 |
| Brass | 102-125 | |
| Copper | 17 | 117 |
| Nickel | 31 | 170 |
| Stainless steel (AISI 302) | 180 | |
| Structural steel (ASTM-A 36) | 200 | |
| Carbon steel | 215 | |
| Titanium (pure) | 16 | |
| Titanium alloy | 105-120 | |
| Wrought iron | 190-210 | |
Swift and Reliable Metal Delivery for Your Every Need
For over two decades, Industrial Metal Service has offered new, mill-sourced metals and verified metal remnants to small metal shop owners and fabricators in the San Francisco Bay Area and beyond. Our wide inventory includes aluminum, titanium, copper, brass, and specialty metals such as Inconel and Hastelloy.
For those who are local, take advantage of our speedy delivery services. We also ship nationwide for those who don’t have the benefit of a local metal supplier, ensuring you get your metals quickly and efficiently, no matter where you are.
Whether you need metals for a quick project turnaround or ongoing production, our commitment to fast delivery means you can keep your operations running smoothly without delays.
 Angle
Angle Cast Plate
Cast Plate Diamond Plate
Diamond Plate Flat Bar
Flat Bar Plate
Plate Round Bar
Round Bar Square Bar
Square Bar Square Tubing
Square Tubing Round Tubing
Round Tubing Angle
Angle Channel
Channel Diamond Plate
Diamond Plate I Beam
I Beam Round Bar
Round Bar Sheet
Sheet Square tubing
Square tubing Round Tubing
Round Tubing Rectangular Tubing
Rectangular Tubing Plate
Plate Rectangular Bar
Rectangular Bar Rectangular Tubing
Rectangular Tubing Round Bar
Round Bar Sheet
Sheet Square Bar
Square Bar Square Tubing
Square Tubing